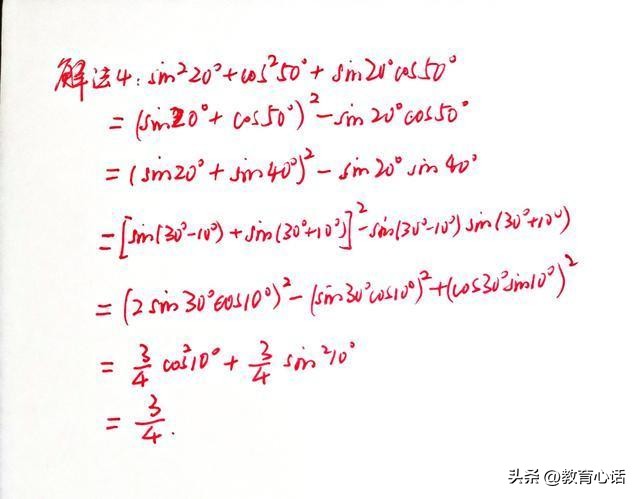cos30度解密：高考数学真题四解法

1995年高考数学真题：三角求值的挑战

大家好！今天我想和大家分享一道1995年高考数学真题。这道题看似简单，但却让现在的许多高中生感到头疼。这是一道三角求值题，我们来看看它的四种常见解法吧。

解法一：降幂公式与二倍角余弦公式

这道题的式子中出现了二次形式，我们可以用降幂公式来处理。如果你记不住降幂公式，也可以用二倍角的余弦公式进行变换。实际上，降幂公式就是从二倍角余弦公式推导出来的。

用降幂公式变换后，原式变为(1-cos40°)/2+(1+cos100°)/2+sin20°cos50°=1+(cos100°-cos40°)+sin20°cos50°。接下来就是难点所在了，当年的学生可以用积化和差和差化积公式来处理，但现在这些公式已经从教材中删除了。

根据积化和差和差化积公式，cos100°-cos40°=-2sin70°sin30°=-sin70°，sin20°cos50°=(sin70°+sin(-30°))/2=(sin70°-sin30°)/2=sin70°/2-1/4。将这些代入前面的式子，就可以得到所求式子的值了。

解法二：配方法

看到这个式子，很多同学第一眼就觉得它像一个完全平方式，所以可以用配方法来求解。先将原式配方，得到(sin20°+cos50°)^2-sin20°cos50°。接下来再用积化和差和差化积公式进行变换，就可以得到所求值了。

解法三：设变量法

我们可以设m=(sin20°)^2+(cos50°)^2+sin20°cos50°，n=(cos20°)^2+(sin50°)^2+cos20°sin50°，然后将两式相加，得到m+n=2+sin20°cos50°+cos20°sin50°。再用两角和的正弦公式，得到m+n=2+sin70°。两式相减，得到m-n=(sin20°)^2-(cos20°)^2+(cos50°)^2-(sin50°)^2+sin20°cos50°-cos20°sin50°。根据二倍角余弦公式和两角差的正弦公式，得到m-n=-cos40°+cos100°+sin(-30°)，再用和差化积公式，得到m-n=-sin70°-1/2。然后就可以求出m的值了。

解法四：诱导公式法

前面三个解法都用到了积化和差和差化积公式，但这些公式已经从现在的教材中删除了。如果没有这些公式，这道题的难度确实会增加不少。

我们先配方，得到(sin20°+cos50°)^2-sin20°cos50°，再由诱导公式得到(sin20°+sin40°)^2-sin20°sin40°。然后再将20°=30°-10°，40°=30°+10°代入，就可以求出答案了。

如果不知道积化和差和差化积公式，这道题确实比较难。但解题的关键还是角的变换，希望这些解法能给大家一些启发。