Binius STARKs解析与优化策略

探索Binius STARKs及其优化：从理论到实践

在加密货币和区块链领域，STARKs（Scalable Transparent ARguments of Knowledge）是一种基于哈希的证明系统，旨在提升去中心化应用（DApps）的性能和可扩展性。然而，现有的STARKs系统在编码效率上仍存在一些不足之处，尤其是对于较小数值的处理。本文将深入探讨Binius STARKs，这可能成为下一代STARKs的典范，其采用二进制域进行直接位操作，显著提高了编码效率和计算性能。

1 引言

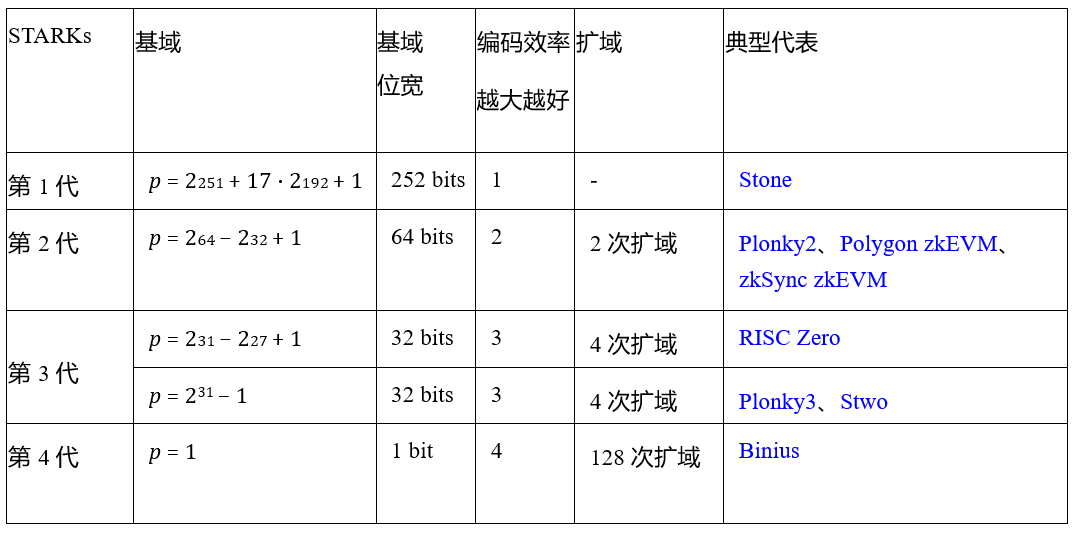
与基于椭圆曲线的SNARKs不同，STARKs可以被看作是基于哈希的SNARKs。当前STARKs效率低下的主要原因之一是，它们在处理实际程序中的小数值（如循环索引、布尔值和计数器）时，效率不高。为了解决这个问题，降低域的大小成为了关键策略。第一代到第三代的STARKs分别使用了252位、64位和32位编码，但这些编码仍然存在大量的浪费空间。相比之下，二进制域允许直接对位进行操作，编码紧凑高效，这使得Binius成为可能的第四代STARKs解决方案。

二进制域的研究可以追溯到上个世纪80年代，并广泛应用于密码学中，如AES、GMAC、QR码等。Binius使用二进制域，完全依赖于扩域来保证其安全性和实际可用性。大多数Prover计算可以在基域下进行，从而在小域中实现高效率。然而，随机点检查和FRI计算仍需进入更大的扩域，以确保所需的安全性。

2 原理解析

当前大多数SNARKs系统的构建通常包含信息理论多项式交互预言机证明（PIOP）和多项式承诺方案（PCS）两部分。PIOP作为证明系统的核心，将输入的计算关系转化为可验证的多项式等式。常见的PIOP协议包括PLONK PIOP、Spartan PIOP和HyperPlonk PIOP等。PCS用于证明PIOP生成的多项式等式是否成立，常见的PCS包括KZG、Bulletproofs、FRI和Brakedown等。根据具体需求，选择不同的PIOP和PCS，并结合合适的有限域或椭圆曲线，可以构建具有不同属性的证明系统。例如，Halo2结合PLONK PIOP与Bulletproofs PCS，基于Pasta曲线；Plonky2结合PLONK PIOP与FRI PCS，基于Goldilocks域。而Binius则结合HyperPlonk PIOP、Brakedown PCS和二进制域，实现了高效性和安全性。

2.1 有限域：基于塔式二进制域的算术化

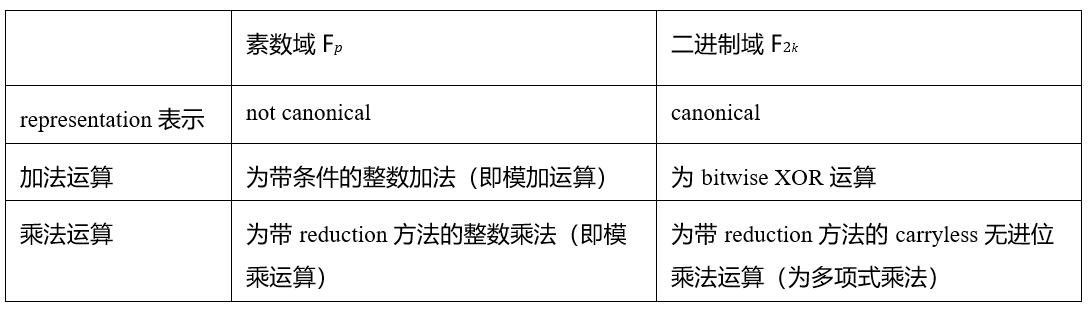
塔式二进制域是实现快速可验证计算的关键，主要归因于其高效计算和简化的算术化过程。在二进制域中，元素的表示方式是规范且直接的，这与素数域不同。素数域无法在给定位数内提供这种规范的表示，而二进制域则具备这种一对一映射的便利性。二进制域在加法和乘法运算中无需引入进位，且平方运算非常高效。例如，一个128位字符串可以在二进制域中以多种方式解释，这不需要任何计算开销，只是位字符串的类型转换。Binius利用这一特性，以提高计算效率。

2.2 PIOP：改编版HyperPlonk Product和PermutationCheck——适用于二进制域

Binius协议中的PIOP设计借鉴了HyperPlonk，采用了一系列核心检查机制，包括GateCheck、PermutationCheck、LookupCheck、MultisetCheck、ProductCheck、ZeroCheck、SumCheck和BatchCheck。这些检查机制用于验证多项式和多变量集合的正确性。Binius在ProductCheck优化、处理除零问题以及跨列PermutationCheck三个方面对HyperPlonk进行了改进。这些改进不仅解决了HyperPlonk中的局限性，还为未来基于二进制域的证明系统奠定了基础。

2.3 PIOP：新的multilinear shift argument——适用于布尔超立方体

在Binius协议中，虚拟多项式的构造和处理是关键技术之一。Packing方法通过将词典序中相邻位置的较小元素打包成更大的元素来优化操作。移位运算符则重新排列块内的元素，基于给定偏移量进行循环移位。这些方法在处理虚拟多项式时保持一致性和效率，适用于布尔超立方体中的高维场景。

2.4 PIOP：改编版Lasso lookup argument——适用于二进制域

Lasso协议允许证明方承诺一个向量，并证明其所有元素均存在于一个预先指定的表中。Lasso解锁了“查找奇点”的概念，并能适用于多线性多项式承诺方案。其证明效率高，且无需承诺大表。Binius将Lasso适应于二进制域的操作，引入了乘法版本的Lasso协议，以确保协议的安全性。

2.5 PCS：改编版Brakedown PCS——适用于Small-Field

Binius多项式承诺主要使用小域多项式承诺与扩展域评估、小域通用构造和块级编码与Reed-Solomon码技术。小域多项式承诺与扩展域评估确保了每个多线性多项式属于域K[X0,...,Xℓ−1]，而评估点可以位于更大扩展域L中。小域通用构造通过定义参数ℓ、域K及其相关的线性块码C，确保扩展域L足够大，以支持安全评估。块级编码与Reed-Solomon码技术允许小域多项式的高效承诺，而不会产生通常与大域相关的高计算开销。

3 优化思考

为了进一步提升Binius协议的性能，本文提出了四个关键优化点：基于GKR的二进制域乘法、ZeroCheck PIOP优化、Sumcheck PIOP优化和PCS优化。这些优化点旨在降低承诺开销、提高计算效率和减少证明大小，从而提升协议的整体性能。

3.1 GKR-based PIOP：基于GKR的二进制域乘法

Binius论文引入了一种基于lookup的方案，旨在实现高效的二进制域乘法运算。然而，这种算法仍需与limbs数量线性相关的辅助承诺。基于GKR的整数乘法运算算法通过将“检查2个32-bit整数A和B是否满足A·B =? C”转换为“检查中(gA)B =? gC是否成立”，大幅减少承诺开销。与之前的Binius lookup方案相比，基于GKR的二进制域乘法运算只需一个辅助承诺，并且通过减少Sumchecks的开销，使该算法更加高效。

3.2 ZeroCheck PIOP优化：Prover与Verifier计算开销权衡

ZeroCheck PIOP优化在证明方和验证方之间调整工作量的分配，提出了多种优化方案，以权衡开销。通过减少证明方的数据传输和评估点的数量，降低了计算和传输成本。此外，代数插值优化进一步提高了效率，使得成本降低了约5/3倍。

3.3 Sumcheck PIOP优化：基于小域的Sumcheck协议

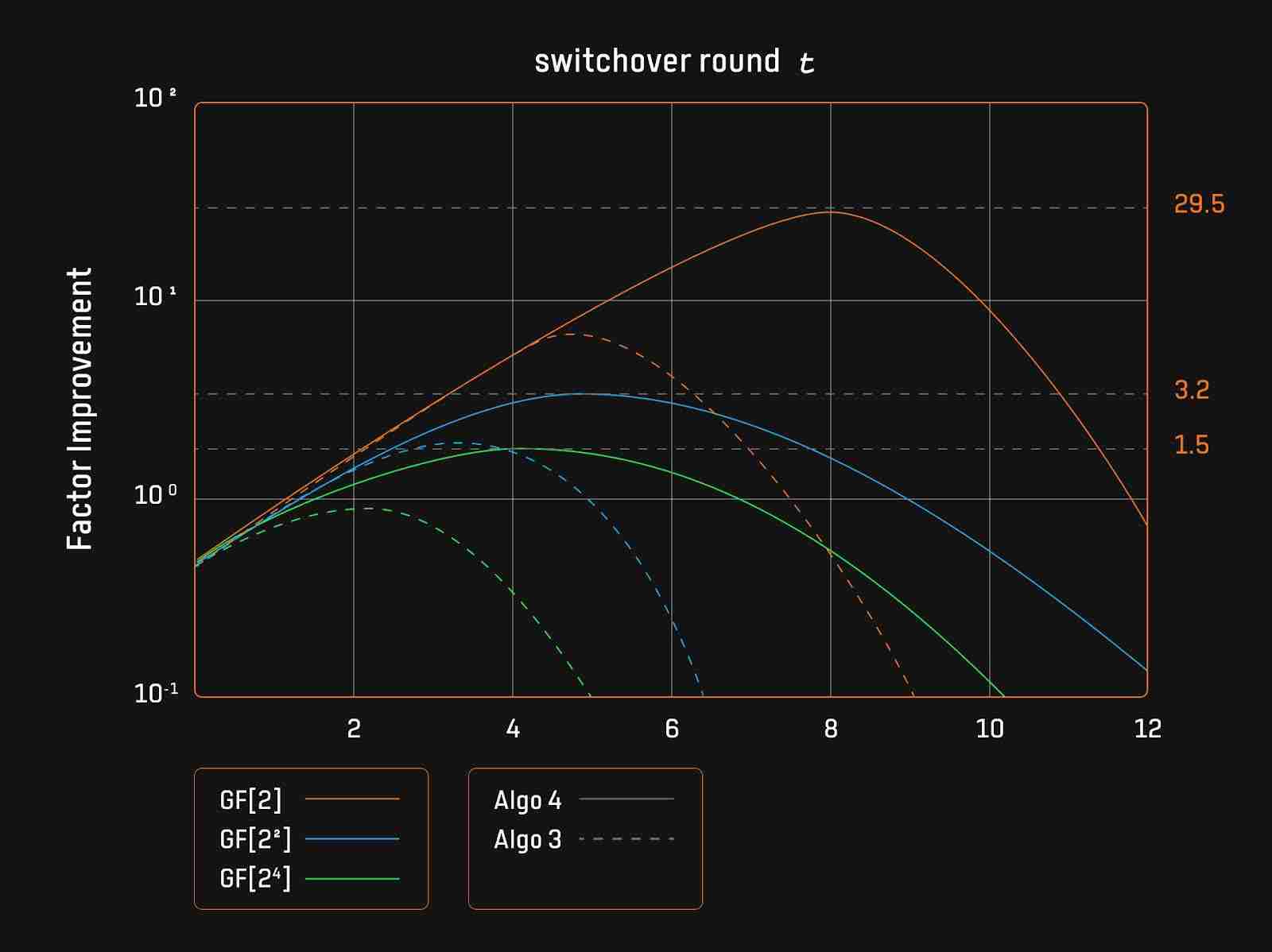
Binius所实现的STARKs方案，其承诺开销很低，使得prover瓶颈不再是PCS，而在于sum-check协议。Ingonyama在2024年提出了针对基于小域的Sumcheck协议的改进方案，并开源了实现代码。这些改进集中于切换轮次t的选择，实验表明，在最佳切换点时，改进因子达到最大值。较小的基域（如GF[2]）能够使优化算法显示出更显著的优势，Karatsuba算法在提升性能方面表现出显著的效果。此外，基于小域的Sumcheck协议在内存效率方面也表现出显著的优势，适用于资源有限的客户端证明环境。

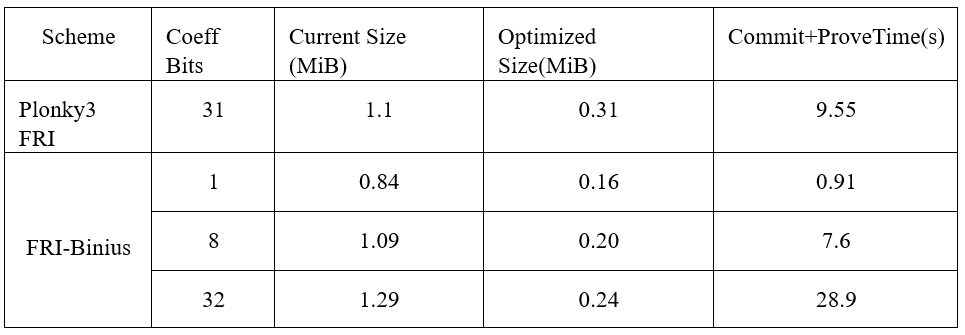
3.4 PCS 优化：FRI-Binius降低Binius proof size

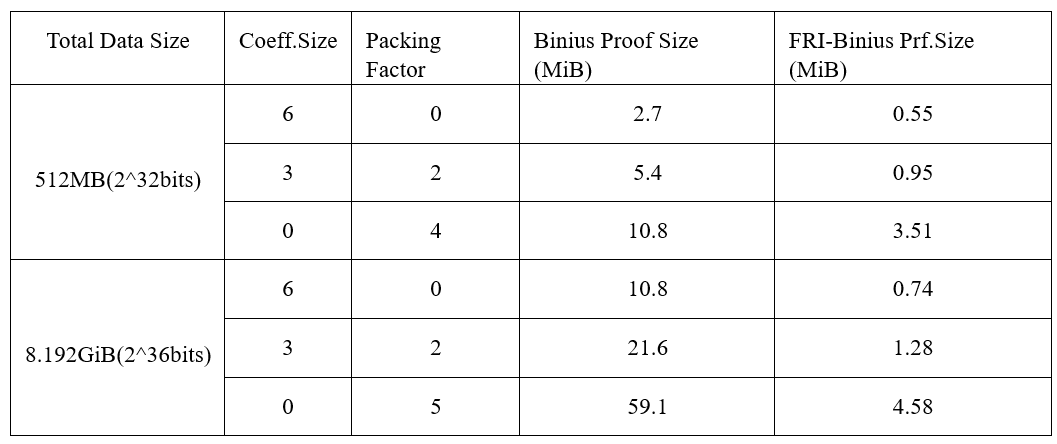
Binius协议的一个主要缺陷在于其相对较大的证明大小。FRI-Binius实现了二进制域FRI折叠机制，带来四方面的创新：扁平化多项式、子空间消失多项式、代数基打包和环交换SumCheck。通过将初始的二进制域多线性多项式打包为定义在更大域K上的多线性多项式，FRI-Binius能够将Binius证明大小减少一个数量级。这使得Binius的证明大小更加接近最先进的系统，同时保持与二进制域的兼容性。

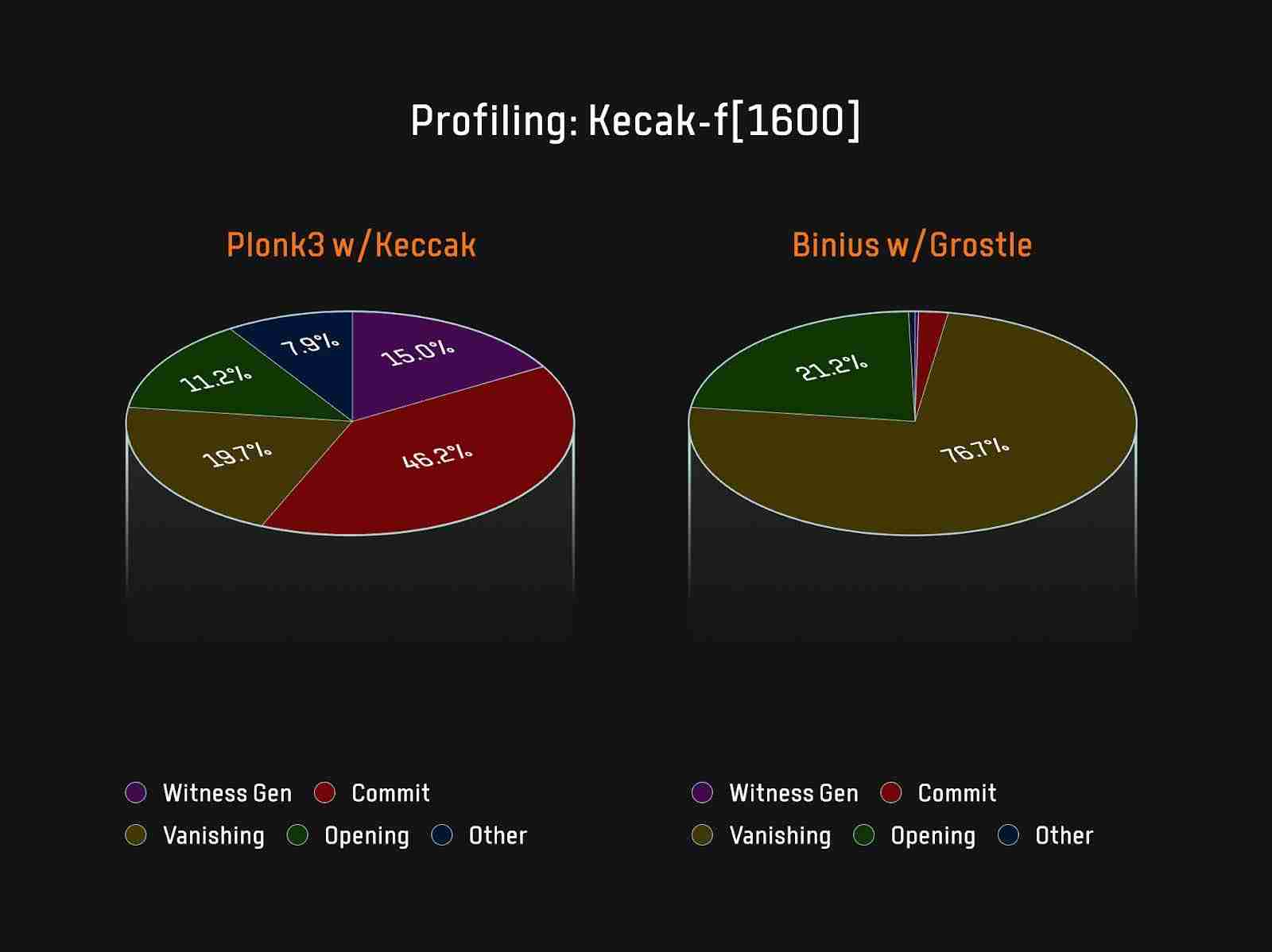
4 小结

Binius的整个价值主张是，可为witnesses使用最小的power-of-two域，因此只需根据所需来选择域大小。Binius是“使用硬件、软件、与FPGA中加速的Sumcheck协议”的协同设计方案，可以以非常低的内存使用率来快速证明。Halo2和Plonky3等证明系统有四个占用大部分计算量的关键步骤：生成witness数据、对witness数据进行承诺、vanishingargument、openingproof。Binius中已基本完全移除了Prover的commit承诺瓶颈，新的瓶颈在于Sumcheck协议，而Sumcheck协议中大量多项式evaluations和域乘法等问题，可借助专用硬件高效解决。FRI-Binius方案为FRI变体，提供了从域证明层中消除嵌入开销的选择。当前，Irreducible团队正在开发其递归层，并与Polygon团队合作构建Binius-based zkVM；JoltzkVM正从Lasso转向Binius，以改进其递归性能；Ingonyama团队正在实现FPGA版本的Binius。